-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaNovel Approach Identifies SNPs in and with Evidence for Parent-of-Origin Effect on Body Mass Index
Large genetic association studies have revealed many genetic factors influencing common traits, such as body mass index (BMI). These studies assume that the effect of genetic variants is the same regardless of whether they are inherited from the mother or the father. In our study, we have developed a new approach that allows us to investigate variants whose impact depends on their parental origin (parent-of-origin effects), in unrelated samples when the parental origin cannot be inferred. This is feasible because at genetic markers at which such effects occur there is increased variability of the trait among individuals who inherited different genetic codes from their mother and their father compared to individuals who inherited the same genetic code from both parents. We applied this methodology to discover genetic markers with parent-of-origin effects (POEs) on BMI. This resulted in six candidate markers showing strong POE association. We then attempted to replicate the POE effects of these markers in family studies (where one can infer the parental origin of the inherited variants). Two of our candidates showed significant association in the family studies, the paternal and maternal effects of these markers were in the opposite direction.
Published in the journal: . PLoS Genet 10(7): e32767. doi:10.1371/journal.pgen.1004508
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1004508Summary
Large genetic association studies have revealed many genetic factors influencing common traits, such as body mass index (BMI). These studies assume that the effect of genetic variants is the same regardless of whether they are inherited from the mother or the father. In our study, we have developed a new approach that allows us to investigate variants whose impact depends on their parental origin (parent-of-origin effects), in unrelated samples when the parental origin cannot be inferred. This is feasible because at genetic markers at which such effects occur there is increased variability of the trait among individuals who inherited different genetic codes from their mother and their father compared to individuals who inherited the same genetic code from both parents. We applied this methodology to discover genetic markers with parent-of-origin effects (POEs) on BMI. This resulted in six candidate markers showing strong POE association. We then attempted to replicate the POE effects of these markers in family studies (where one can infer the parental origin of the inherited variants). Two of our candidates showed significant association in the family studies, the paternal and maternal effects of these markers were in the opposite direction.
Introduction
The effect of genetic variants on phenotypes may depend upon the parent from whom the variant was inherited [1], [2]. Parent-of-origin effects (POEs) may arise through imprinting; mechanisms of which include cytosine methylation and histone deacetylation [2]. To date around 50 human genes are known to be imprinted and for most mammalian species less than 1% of the genome is confirmed to be imprinted [3]. One plausible explanation for this phenomenon is the parental conflict hypothesis, whereby both parents would like to maximize the influence of their genome on their offspring [4]. Current methods for detecting parent-of-origin effects rely on assigning parental ancestry to the inherited alleles. This is straightforward in linkage studies, which have identified potential POEs on type 2 diabetes, body mass index (BMI) [5], [6], and alcohol intake [7]–[9]. However, only a very few of these findings have been replicated and the identified linkage peaks often span large chromosomal regions harbouring hundreds of genes, hence the causal gene or regulatory sequence is unknown. A notable exception is the work of Kong et al [1] who inferred parental origin through genealogy information and long-range phasing to subsequently test for POEs. This study identified six SNPs, four associated with risk of type 2 diabetes and the other two associated with each of breast cancer and basal-cell carcinoma.
Genome-wide association studies (GWASs) of unrelated individuals have very precisely identified a large number of genetic loci harbouring SNPs whose (alternative) allele counts associate with common traits. Since GWASs predominantly include unrelated individuals, the parental origin of the alleles cannot be determined, hence genetic effects influenced by the parental origin of the alleles are typically not considered. Here we present a novel approach that is able to detect POEs using genome-wide genotype data of unrelated individuals. We chose BMI as our target trait, due to previous findings [5], [6] and the large available sample size. We report the discovery of two novel loci affecting BMI in a manner dependent on the parent-of-origin of the transmitted alleles.
Results
We applied our POE test, which compares the phenotypic variance of the heterozygous genotype group to the variance observed in the homozygous groups, to all SNPs genome-wide. The test, which is applicable to unrelated individuals, assumes that an increased variance in the heterozygous group arises because the heterozygous group consists of two subgroups (paternal reference allele/maternal alternative allele and maternal reference allele/paternal alternative allele) each with different means (see Figure 1). Differences in phenotypic variance were tested using the Brown-Forsythe test, modified to test the mean absolute deviations from the median in the heterozygous and homozygous groups (see Materials and Methods for details). We applied this test to BMI values (corrected for age and age-squared), separately in men and women, in 15 studies, totalling up to 56,092 individuals (detailed description of the cohorts can be found in Tables S1–S3), 13 of which participated in previous meta-analyses of the GIANT consortium [10]. In total 2,673,768 HapMap imputed and genotyped SNPs were tested. For each locus, a lead SNP (with the strongest POE association) was identified; other markers within 1 Mb or in LD (r2>0.1) were excluded from further investigations. Sex-specific association summary statistics were then meta-analysed. No sex specific difference in effects were observed, therefore all reported results are sex-combined.
Fig. 1. Explanation of the POE test. 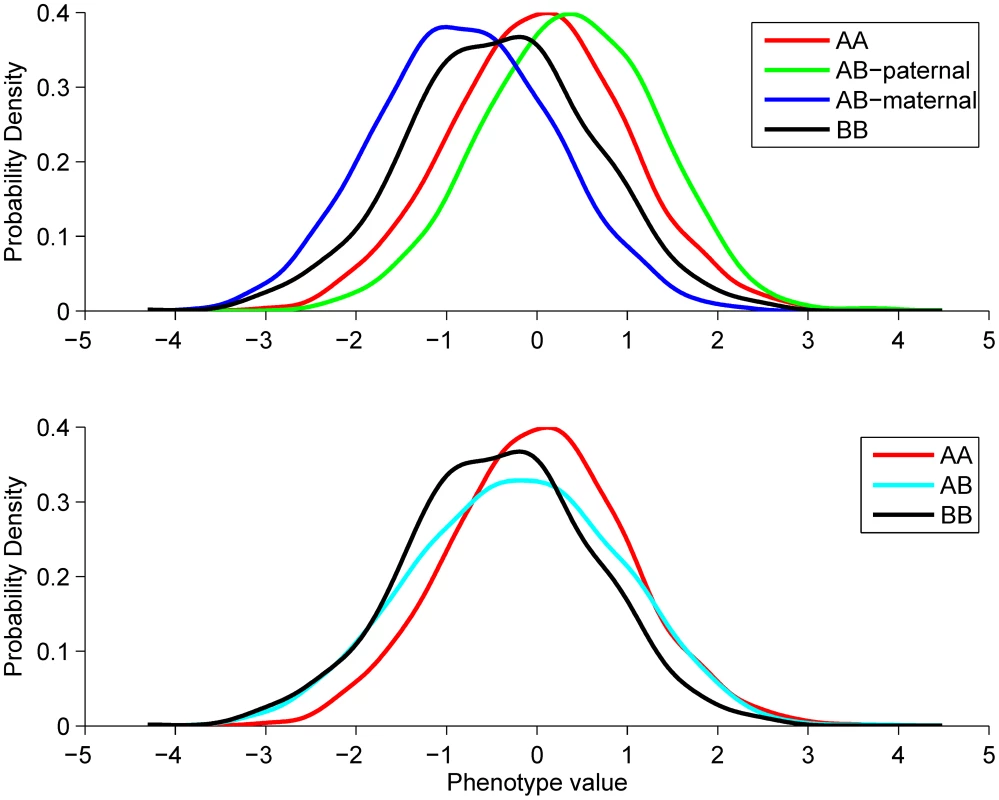
Top panel illustrates the phenotype distributions in the four genotype groups that would be observed if the parent-of-origin of the alleles were known. Bottom panel shows how these distributions change if the parent-of-origin is unobserved. The resulting heterozygous group will have increased variance due to its heterogeneity. This example describes a scenario we observe for the two replicated hits, namely that the paternal- and maternal effects are of the same size, but opposite in direction (). Therefore the average phenotype in the B/B group is the same as in the A/A group, as the paternal and maternal B allele effects cancel each other out. In the A/B group there are two subpopulations: the A-pat/B-mat group with phenotypic mean of and the A-mat/B-pat group with mean. Thus, the two subpopulations combined also have zero mean, but increased variance. Our criteria to select SNPs to take forward to the replication stage resulted in the selection of six independent SNPs: four lead SNPs with POE P-value <5×10−6 and three SNPs in imprinted regions with P<5×10−4 (see Fig S1 for QQ-plot), one SNP fulfilled both criteria. See Table 1 for details of these results and Materials and Methods for details of the applied selection methods. These six SNPs were carried forward to the replication stage.
Tab. 1. Discovery POE association results for the six SNPs selected for replication. 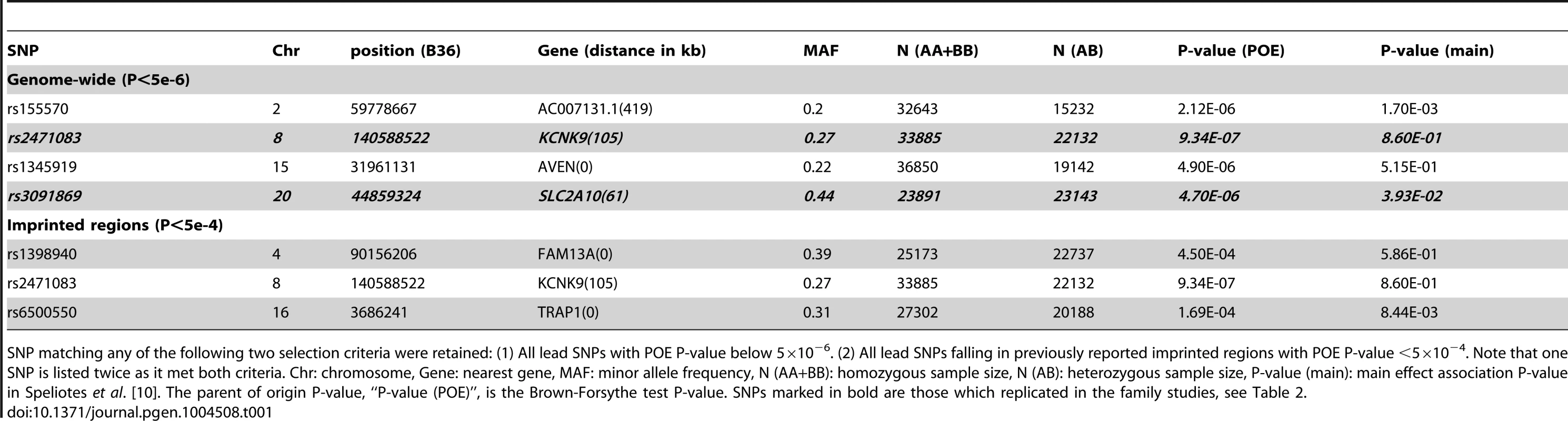
SNP matching any of the following two selection criteria were retained: (1) All lead SNPs with POE P-value below 5×10−6. (2) All lead SNPs falling in previously reported imprinted regions with POE P-value <5×10−4. Note that one SNP is listed twice as it met both criteria. Chr: chromosome, Gene: nearest gene, MAF: minor allele frequency, N (AA+BB): homozygous sample size, N (AB): heterozygous sample size, P-value (main): main effect association P-value in Speliotes et al. [10]. The parent of origin P-value, “P-value (POE)”, is the Brown-Forsythe test P-value. SNPs marked in bold are those which replicated in the family studies, see Table 2. Replication in family-based studies
The replication stage utilised five family-based studies (see Tables S1–S3) to test for parent-of-origin effects at the six selected SNPs. Only heterozygous individuals are informative when testing for parent-of-origin effects; the number of heterozygous individuals for each of the tested SNPs ranged from 1,122 to 4,128 (see Table 2 and Table S4). A simplified parental asymmetry test (PAT, see Materials and Methods) was applied and SNPs successfully replicated if their PAT P-values were below 0.0083 (Bonferroni corrected significance threshold for family-wise error of 0.05 with six tests). Two of these SNPs, rs2471083 [T/C] (GWAS discovery BMI variance (het vs. hom): 1.058 vs 0.963, PPOE = 9.34×10−7; replication PAT P = 0.00264) and rs3091869 [T/C] (GWAS discovery BMI variance (het vs. hom): 1.046 vs 0.957, PPOE = 4.7×10−6; replication PAT P = 0.00245) successfully replicated. In particular, we found that heterozygous individuals who carry the rs2471083-C allele paternally have 0.11 (SD unit) higher BMI on average than those carrying the C-allele maternally (P = 0.00264). Heterozygous carriers of the paternal rs3091869-C allele have 0.11 (SD unit) lower BMI on average than those carrying the maternal C-allele (P = 0.00245). Figure 2 shows the locuszoom plots of the POE association P-values for the two replicated loci (KCNK9 and SLC2A10).
Fig. 2. Local association plots. 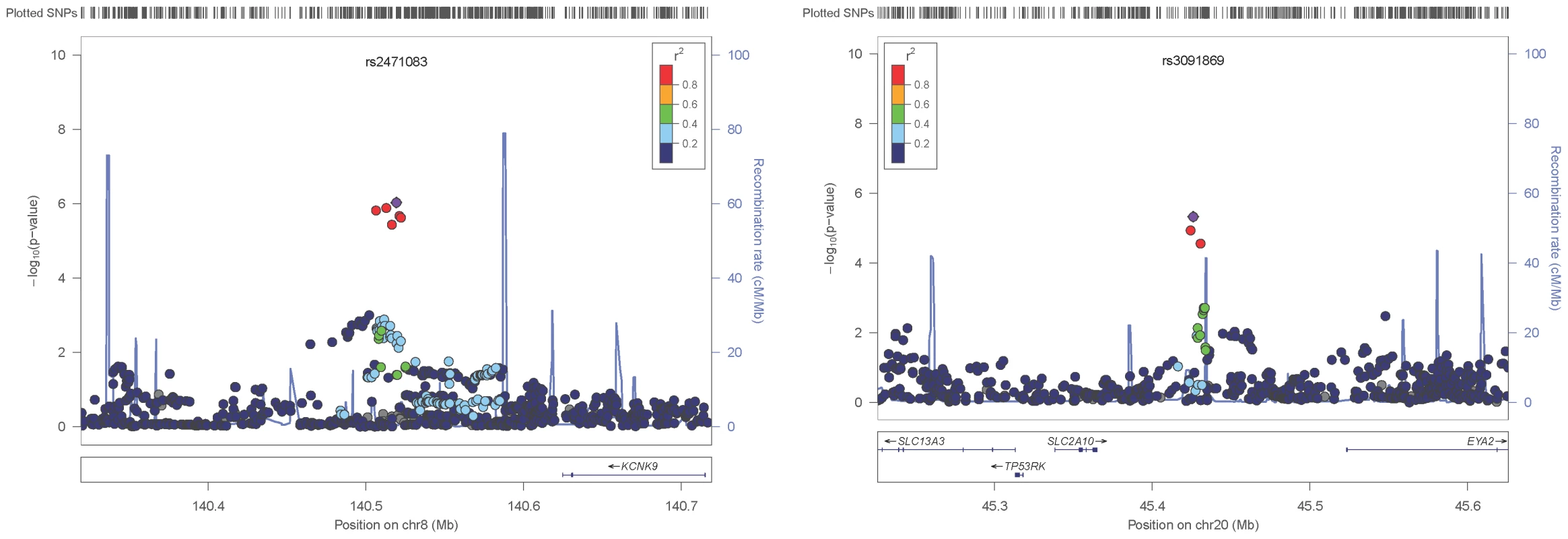
Panels show the local POE association P-values for the KCNK9 (left panel) and SLC2A10 (right panel) loci. Tab. 2. Replication of the 6 discovery SNPs in trios (or parent-offspring pairs). 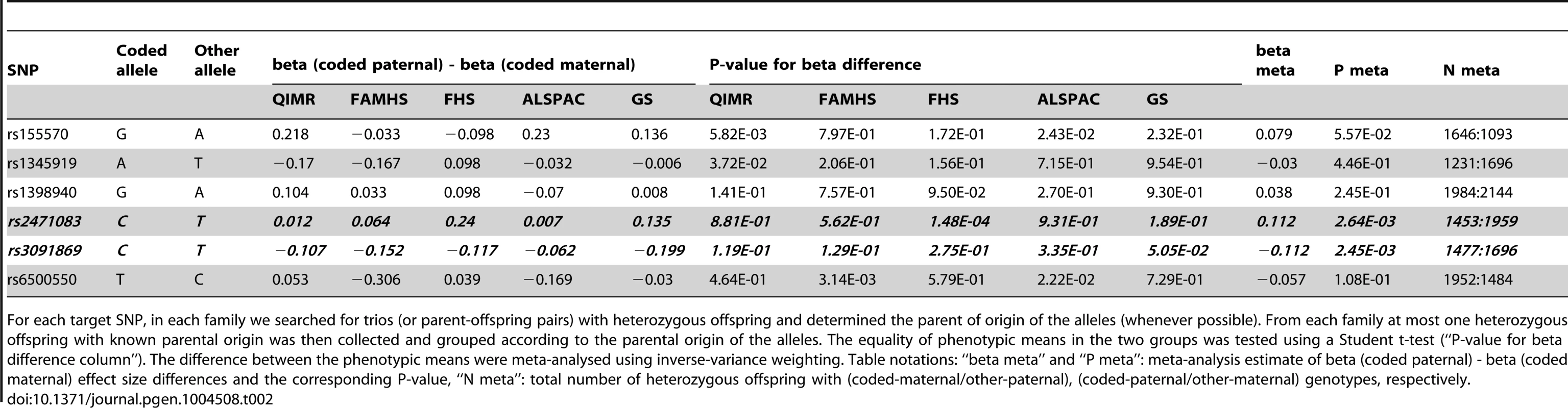
For each target SNP, in each family we searched for trios (or parent-offspring pairs) with heterozygous offspring and determined the parent of origin of the alleles (whenever possible). From each family at most one heterozygous offspring with known parental origin was then collected and grouped according to the parental origin of the alleles. The equality of phenotypic means in the two groups was tested using a Student t-test (“P-value for beta difference column”). The difference between the phenotypic means were meta-analysed using inverse-variance weighting. Table notations: “beta meta” and “P meta”: meta-analysis estimate of beta (coded paternal) - beta (coded maternal) effect size differences and the corresponding P-value, “N meta”: total number of heterozygous offspring with (coded-maternal/other-paternal), (coded-paternal/other-maternal) genotypes, respectively. Impact of the discovered variants
By combining the effect difference estimates from the family-based studies and the marginal association effect sizes from the largest-to-date meta-analytic study on BMI [10], we estimated the effects of the maternal and paternal alleles. For both rs2471083-C and rs3091869-T we obtained and . Using these effect sizes and the population frequency of these SNPs, we calculated the explained variance of these SNPs (if their parent of origin is known) to be 0.24% and 0.30% for rs2471083 and rs3091869, respectively. These effects are comparable to that of the strongest BMI-associated variant in the FTO gene (0.34%) [10].
Notably, rs2471083 is located 105 kb upstream of the imprinted gene KCNK9. Mutations in this potassium channel gene cause Birk-Barel syndrome, a maternally transmitted syndrome of mental retardation, hypotonia, and unique dysmorphism, resulting from genomic-imprinting [11]. SNPs within 2 kb have been shown to be associated with HDL cholesterol, adiponectin levels [12] and blood pressure [13]. Its impact on hypertension is potentially via a mechanism involving aldosterone, the concentration of which correlates strongly with fat mass. Interestingly, KCNK9 knock-out mice exhibited more fragmented sleep episodes [14] and 7.1%–9.6% increased weight gain (P = 0.02) at 19–20 weeks of age [15]. SNP rs3091869 is 61 kb upstream of SLC2A10, a glucose transporter involved in arterial morphogenesis. SNPs in low LD (in CEU r2 = 0.05) with rs3091869 have been shown to alter body fat distribution [16].
We tested these two confirmed SNPs in 705 trios with paediatric (extreme) obese offspring in which parental origin of the alleles was known in up to 255 individuals [17]. No significant effect was observed (see Table S5). This could be due to insufficient power, different genetic mechanisms between young individuals and adults or that our association is specific to variations within the range of normal BMI.
Expression experiments
We evaluated whether the parent of origin effect of the rs2471083-T and rs3092611-T (proxy for rs3091869-T, r2 = 0.998) alleles can be observed in the expression levels of their respective genes (KCNK9 or SLC2A10). To test this we carried out quantitative PCR (qPCR) experiments using lymphoblastoid cell lines (LCL) of the CEPH families. These cell lines have been used extensively to identify imprinted genes [18], [19]. Using the available trio data we could infer the parental origin of the alleles of rs2471083 and rs3092611 in 33 (9 maternal T alleles, 24 paternal T alleles) and 24 (16 maternal T alleles, 8 paternal T alleles) individuals respectively (Table S7). We performed between 2 and 10 technical replicates per individual (mean of 7.75) and samples with high coefficient of variation (>5%) were discarded in order to ensure robustness. After quality control, 124 expression values from 23 (mat:pat = 4∶19) samples for KCNK9 and 240 expression values from 24 (mat:pat = 16∶8) for SLC2A10 were available for analysis. We fitted a linear mixed model to test for association between expression levels (Ct values) and allelic origin. The paternal T allele of rs2471083 was associated with lower KCNK9 expression levels (+1.08 [SD unit] Ct values, P = 0.0096), and the paternal T allele of rs3092611 was associated with higher SLC2A10 expression values (−1.09 [SD unit] Ct values, P = 0.0023). To ensure there was no systematic bias in our experiments giving rise to spurious POE associations we repeated the qPCR experiments for two housekeeping genes GAPDH and HRPT1. Both analyses gave non-significant POE P-values (P>0.3).
Methylation lookups
POEs can be driven by differences between inherited paternal and maternal methylation. To explore whether the observed parent-of-origin effects at our discovered SNPs were driven by differential methylation we tested whether methylation in the regions (Chr8 : 140.45–140.65 Mb and Chr20 : 45.3–45.55 Mb) was (i) associated with the two respective SNPs (rs2471083, rs3091869) in 262 unrelated individuals from the TwinsUK cohort and (ii) associated with BMI in two independent cohorts: 79 BMI discordant (difference >0.5 SD) monozygotic twin pairs from the TwinsUK cohort and a sample of 412 unrelated individuals from the EPIC-Italy cohort. None of these analyses showed significant association (see Supplemental Data S1, Figures S2, S3 and Table S8 for further details).
Discussion
Our novel approach revealed two SNPs, located near the genes KCNK9 and SLC2A10, influencing BMI in a parent-of-origin specific fashion. These loci were the first and fourth most significant genome-wide in our new POE test for unrelated individuals and both showed significant parent-of-origin effects in family studies. Both SNPs exhibit polar overdominance, where homozygous individuals have equal (baseline) phenotypes and heterozygous genotypes confer relative risk/protection, depending on the parental origin. Polar overdominance, has been observed in humans for type2 diabetes [1] and BMI [20], however it is very rare and its molecular mechanism is unknown.
RT-PCR experiments revealed that gene expression levels of KCNK9 and SLC2A10 in LCLs were also influenced in a parent-of-origin manner. The expression of these genes is highest in the brain (although it is also expressed in testis, liver, colon, adrenal gland and kidney; see http://www.genecards.org/) indicating a potential neuronal involvement. Expression levels of KCNK9 and SLC2A10 in living brain cells might have been more informative and robust, however, such information is not available. The applied qPCR method was optimised to ensure that the expression levels measured in LCLs were representative only of the target transcript and amplification efficiency was assessed to be sensitive enough to allow the detection of even small changes in gene expression. Interestingly, rs2471083 alleles, regardless of their parental origin, show marginally significant association (P = 0.03) with KCNK9 expression levels in the hippocampus (http://www.broadinstitute.org/gtex/). Our methylation analyses did not reveal any evidence that the POEs were driven by differences in inherited paternal and maternal methylation. Neither of our two SNPs tag common copy number variants (CNVs) (based on the CNV reference data used in Heid et al. [21]) and we found only one sample (out of 14,315 available in-house, whose BMI Z-score was +1.18) with a 76 kb deletion overlapping rs2471083. Hence, the effect of the two discovered SNPs are unlikely to be driven by CNVs. To check whether the two confirmed SNPs (rs3091869, rs2471083), or SNPs in LD (10 with r2>0.8 in 1000 Genomes EUR population), show regulatory activity, we queried RegulomeDB (http://regulome.stanford.edu). None of these SNPs were annotated to have more than minimal binding evidence (RegulomeDB score below 4).
A previous study proposed to detect POE in inbred F2 mice by a two-component mixture distribution fitting of the heterozygous genotype group and further two components for the homozygous groups [22]. This method requires a parametric distribution of the phenotype to be assumed, small violations of this assumption can result in heavily biased parameter estimates. The method we chose is more robust to a wide range of phenotype distributions (due to the underlying Brown-Forsythe test employed), computationally faster (making it attractive for testing millions of SNPs) and applicable to probabilistic genotype calls. Our POE test for unrelated GWAS samples is similar to a test proposed to detect gene-environment interactions [23] in that it exploits differences in phenotypic variance to detect a phenomenon not directly measured. Inflated phenotypic variance in the heterozygous group might also be the result of other phenomenon: (i) a phenotype altering effect (be it genetic or environmental) acting only on the heterozygous group; (ii) an overdominant effect combined with a genetic or environmental interaction or non-linear, monotonic phenotype transformation that has different derivatives for low and high trait values; (iii) a large marginal additive effect combined with a (monotonic) transformation for which the second derivative is maximised at the mean phenotype value of the heterozygous group (see Materials and Methods for details). More generally, the combination of the scale on which the phenotype is measured and a strong marginal association with an allelic dosage may give rise to spurious associations using variance tests [24]. Recently some evidence has emerged about loci which effect the variance of phenotypes (through impacting environmental plasticity, canalization, developmental stability, etc.) that can be detected via association with phenotypic variability [25]. Therefore, the top hits obtained by our POE test may need further prioritisation before proceeding to trio-based confirmation. We recommend the following checks: (a) Exclude SNPs with overdominant effects; (b) For SNPs with low POE P-value, test gene-environment (GxE) interaction (as done in [23]) via modelling phenotypic variance as a function of the genotype dosage (coded in additive, recessive or dominant fashion). If this test is more significant than the POE test, it is probably a GxE that is driving the POE association and also as a side effect we will observe significant difference in the variance between the two homozygous groups. (c) If a SNP with low POE P-value has marginal effect on the trait, repeat the POE test for various transformed versions of the phenotype such as log and inverse-normal quantile. If the resulting POE P-values are not robust, give lower priority to the examined SNP.
For our confirmed SNPs multiple lines of evidence show that the parent-of-origin effects are real, most convincingly clear replication in independent family data of parent-of-origin associations of the hit SNPs with both BMI and gene expression levels. Further, the GWAS discovery associations are very unlikely to be artefacts of the factors discussed above: (i) there is no evidence of overdominant, additive, recessive or dominant effects (the mean BMI values are near identical in the three genotype groups), hence the signals cannot be driven by gene-environment interactions or be an artefact of the scale on which the phenotype is measured (ii) no SNP within 500 kb has any detectable marginal effect on BMI thus the association cannot be driven by haplotype-specific marginal effects [26]; (iii) the phenotypic variances in the two homozygous groups, are almost identical (rs2471083: , , and rs3091869: , , ); (iv) POE test with log - and inverse-normal quantile transformed BMI values resulted in similar results (Table S6), further reducing the likelihood of an artefact resulting from the scale on which the phenotype is measured [24].
Some of the negative results of the other SNPs carried forward to the replication phase in the family data could be explained by lack of power. The power to replicate POE associations in family-based studies is dependent on the available number of heterozygous individuals (for details see Supplemental Data S1) and thus increases with minor allele frequency (MAF). Therefore, it is unsurprising that the two SNPs which replicated had relatively high MAF (>27%).
Linkage studies have identified four regions exerting POE on BMI (10p12, 12q24, 13q32) [5] and 2q31 [27]). We looked up SNPs in these regions in our genome-wide discovery POE association results. The reported linkage regions showed enrichment for lower than expected POE P-values (see Figure S4 for regional QQ-plots), however, no SNPs survived Bonferroni correction. We also tried to replicate a SNP in exon 5 of DLK1 (rs1802710) because this SNP showed polar overdominance for obesity in children [20], but only a very slight trend (P = 0.32) was visible in our study. Previously reported BMI-associated loci [10] show some enrichment for lower POE P-values (Supplemental Data S1, Tables S9, S10 and Figure S5), however these need to be replicated in family studies.
Previous work comparing strength of associations of mother-offspring BMI with father-offspring BMI did not reveal intrauterine influence on obesity in children [28]. A similar conclusion was reached in a systematic review of seven studies [29], while stronger maternal influence was observed in a recent longitudinal study [30]. The difference in conclusions may be due to that fact that the former studies included predominantly older children than the longitudinal study (0–3.5 years). At early age the diet of the offspring may be more similar to that of the mother than the father (e.g. due to breastfeeding), which might have contributed to the higher mother-offspring BMI similarity found by Linabery et al. [30].
In summary, our findings indicate that POEs may play a role in adult obesity. The two identified SNPs have strong parent-of-origin effect on BMI, close to that of the FTO, contributing substantially to the heritability of BMI. Our follow-up experiments demonstrated parent-of-origin specific gene expression modulation, but failed to link methylation activity of these loci to BMI values. Inevitably for newly discovered loci, further studies are warranted to determine how these variations functionally influence obesity in humans. The reliance of our approach on difference in phenotypic variance means that it cannot be extended to binary outcomes. Since there are other phenomena which can give rise to significant POE association, we recommend that top hits from our method are followed up in family studies, where parental origin of alleles can be inferred. In addition, our variance based POE test for GWAS data is naturally much less powerful than actually testing the mean values of the two heterozygous subgroups in trios. However, GWASs of unrelated individuals are several-fold more numerous and typically much larger than studies with a trio design, hence our methodology provides a great advance in parent-of-origin research by providing means to exploit all available GWAS data of unrelated individuals in order to identify parent-of-origin effects on continuous phenotypes.
Materials and Methods
Ethics statement
All participating studies were approved by the respective institutional Ethics Committees. All study participants gave written consent including for genetic studies.
Detecting parent of origin effects
If we denote the alleles of a bi-allelic SNP by “A” (reference) and “B” (alternative) the possible genotypes are A/A, A/B and B/B. Standard GWASs estimate the effect of the alternative allele dosage on the phenotype in question. In this work we are interested in associations in which a phenotype (y) is influenced by the alleles of a particular SNP and the effect depends on the parental origin of these alleles. In the presence of a parent-of-origin effect the heterozygous genotype group is split into two subgroups, depending on the parental origin of the A and B alleles. We assume that the phenotype of any individual in the A/A genotype group is modelled by , where is the mean and is an individual level error with mean zero and variance . If the maternal and paternal effects of the B allele are and, it follows that the phenotype of an individual in the B/B group is and its variance is . (Note that as a consequence the maternal and paternal effects of the A allele are and .) Here we assume is constant across genotype groups (A/A, A/B and B/B) and and are fixed effects. The effects of violations of these assumptions are covered in the discussion. The phenotype in the heterozygous group is a 50%–50% mixture of two distributions (Fig 1a):
where is a Bernoulli random variable (with parameter ½), taking values if the B allele is inherited from the mother and if inherited from the father. The heterozygous phenotype distribution can be simplified to Since and are independent random variables, the phenotypic variance of the heterozygous genotype group isIf a parent-of-origin effect is present andare different, thus is larger than the variance observed in the homozygous groups () (Figure 1). Therefore, although in regular GWAS data we cannot identify the two subgroups within A/B genotypes, we can detect POE via increased phenotypic variance in the heterozygous group relative to the homozygous groups.
In the presence of a marginal association a phenotype transformation could alter the genotype group variances and introduce bias into the test [24]. For this reason we analysed untransformed age-, age2-corrected BMI values (normalised to have zero mean and unit variance) separately for men and women. Standard variance tests (such as the F-test) are, however, sensitive to deviations from the Gaussian distribution.
Therefore, we used a robust version of the Brown-Forsythe test. Briefly, we first centred the phenotype values (at zero) in each genotype group to avoid inflated variance in the presence of marginal effects in the group of all homozygote individuals. We denote these centred phenotypes by , where
Here stands for the genotype of individual , and represents the median phenotype value in genotype group , where can take the values of AA, AB or BB. We then regress the absolute deviations from the median onto a 0–1 coded genotype group identifier (1 for heterozygous and 0 for homozygous individuals) in order to estimate the POE effect size [31]. This regression result in a slope estimate
where and . The corresponding standard error is whereFinally, the POE P-value is assigned based on the test statistic . The test was extended to imputed genotype probabilities and implemented in the latest version (v0.98) of the Quicktest software (http://www3.unil.ch/wpmu/sgg/quicktest/). The robustness of this test to deviations from normality has been studied in [32] and its power in [31].
SNP selection strategy
We applied our POE test genome-wide to all HapMap imputed markers in a set of cohorts and results were combined across cohorts using fixed-effect inverse-variance weighting meta-analysis. SNPs were selected for replication if they met at least one of the following two criteria: (1) POE P-value <5×10−6 or (2) POE P-value <5×10−4 and within 500 kb of previously reported imprinted regions according to the Catalogue of Parent of Origin Effects database (http://igc.otago.ac.nz/home.html). At loci which met either criteria, a lead SNP (with the strongest POE association) was identified; other markers within 1 Mb or in LD (r2>0.1) were excluded from further investigations. In total 2,673,768 HapMap imputed and genotyped SNPs were analysed, of which 29,457 were considered as lying in imprinted regions, criterion (2). Using the procedure of Gao et al. [33] we estimated the effective number of tests considered by each criterion to be ∼1,000,000 and 6,100 respectively, justifying the ∼100 fold drop in the P-value threshold applied to the second criterion.
Testing in family-based studies
We tested our findings in family-based studies using a simplified parental asymmetry test [34] (PAT). For each target SNP, in each family we searched for trios (or parent-offspring pairs) with heterozygous offspring and determined the parent of origin of the alleles (whenever possible, i.e. at least one homozygous parent). From each family at most one heterozygous offspring with known parental origin was then collected and grouped according to the parental origin of the alleles. Note that although POE is acting in every genotype group, it can only be detected in the heterozygous group.
As at the discovery phase, we used sex-, age - and age2-corrected BMI residuals as phenotype. The equality of phenotypic means in the two groups was tested using a Student t-test. When significant differences were detected we also estimated the difference between paternal and maternal effect sizes, which is simply the difference between the phenotype averages in the paternal - and maternal - groups.
Effect size estimation
In order to estimate paternal ) and maternal () effect sizes it is sufficient to know their mean and their difference . The difference between paternal and maternal effect alleles can also be derived from GWAS of unrelated individuals. It is easy to see that the test statistic defined as
gives an unbiased estimate of . Since , the variance of T is . Therefore, the absolute difference in paternal and maternal effects () can be estimated if the phenotypic variances in the three genotype groups are known. However, these estimates will be strongly subject to the winner's curse [35], thus we used the family studies to derive more reliable estimates of . To reduce the effect of differences in the distribution of BMI between the family-based studies, we meta-analysed the difference estimates from each study in order to obtain a combined estimate of . The average of the maternal - and paternal effects, , is the association effect size using a simple additive genetic model, which can be most accurately estimated from the largest-to-date meta-analytic study on BMI [10] (including ∼250,000 individuals).Effect of phenotype transformation in case of marginal association
If there is an additive marginal genetic effect influencing the trait certain transformations may inflate the phenotypic variance of the heterozygous group. Let be the phenotypic mean in the heterozygous group and the marginal effect of the SNP (on the original scale). Let denote an S-shaped transformation function of the form that is applied to the trait.
In the following we show that for any value arbitrarily large phenotypic variance inflation can be achieved in the heterozygous group, compared to the two homozygous groups by an appropriate parameter choice for . Using a second order Taylor expansion the variance of the transformed phenotype in the heterozygous group can be estimated by
If we assume the phenotype follows a Gaussian distribution then, simplifies to and thus
Without loss of generality one can assume that . The variance in AA genotype group can be estimated similarly and thus
Using the special form of , the variance difference can be expressed as
and since andIt is easy to see that for a fixed
As , faster than , thus for any effect size we can find a transformation function such that the variance inflation of the heterozygous group exceeds any arbitrary threshold.
Cell lines, nucleic acids isolation, sequencing and qPCR
Lymphoblastoid cell lines were derived from peripheral blood leukocytes of 95 members of 11 CEPH families [36] (#102, #884, #1333, #1340, #1341, #1345, #1346, #1347, #1362, #1408, #13292). They were purchased from the Coriell Cell Repository (http://ccr.coriell.org/), and cultured as previously described [37]. DNA was extracted by using the QIAamp DNA Mini kit (QIAGEN), and RNA by using the RNeasy Mini kit (QIAGEN), according to the manufacturer's instructions. Primer sequences were designed to amplify a 328-bp region on chromosome 8 that spans the rs2471083 polymorphism (forward primer: 5′-ACCACAGAAGTCAGTAGACGAG-3′; reverse primer: 5′ - GTGACATTGGGAGCATGGGA-3′) and a 146-bp region on chromosome 20 that spans the rs3092611 polymorphism (forward primer: 5′-GCCACCAGTGGTCTGATAGT-3′; reverse primer: 5′ - TAACTCGTCATTCTGCCCTGG -3′). PCR amplification was performed in a 25 µl reaction using GoTaq polymerase (Promega). After purification of PCR products (ExoSAP-IT, USB), sequencing reactions were carried out by using 1 µl of each of the 3.2 µM sequencing primers and 0.5 µl of BigDye Terminator v1.1 (Applied Biosystems). Following on-column purification (EdgeBio), sequencing products were run on an ABI-3130 XLS sequencer (Applied Biosystem). To synthesize cDNA, 2 µg of total RNA was retrotranscribed using the Superscript III reverse transcriptase (Invitrogen/Life Technologies) according to the manufacturer's instructions and a mix of random hexamers and oligo-dT that facilitate the detection of poorly expressed genes. To validate primers for qPCR, we first performed a series of test amplifications by using a defined range of primer concentrations (50–200 nM). We then loaded 10 µl of each qPCR product on 1% agarose gels to check the specificity of the amplification product, which should correspond to a 113-bp (KCNK9) and 148-bp (SLC2A10) fragment. To test KCNK9 and SLC2A10 PCR efficiency a standard curve made of five serial dilutions of brain and lung cDNA were used, respectively, since the two genes are known to be highly expressed in these organs. We obtained a standard curve slope of −3.49 for KCNK9 and of −3.37 for SLC2A10, corresponding to 94% and 98% PCR efficiency. For more details see Supplemental Data S1.
Comparing Ct values
The output of the analysis was threshold cycles (Ct), i.e. the number of cycles at which the fluorescent signal of the reaction crosses a pre-determined threshold value. Since standard quantification methods (including normalization by housekeeping genes) introduce a considerable amount of experimental noise for very lowly expressed genes, raw Ct values were used to perform an absolute quantification of KCNK9 and SLC2A10 transcripts. As negative controls, housekeeping genes (HPRT1, GAPDH) were also tested for parent-origin-effect to exclude the possibility that the observed difference in KCNK9 and SLC2A10 expression levels was due to the sample preparation process. Raw Ct values were inverse-normal quantile transformed and a linear mixed model was fitted (using the R function lmer) modelling the technical replicates as random effects and parental origin as a fixed effect.
Supporting Information
Zdroje
1. KongA, SteinthorsdottirV, MassonG, ThorleifssonG, SulemP, et al. (2009) Parental origin of sequence variants associated with complex diseases. Nature 462 : 868–874.
2. RampersaudE, MitchellBD, NajAC, PollinTI (2008) Investigating parent of origin effects in studies of type 2 diabetes and obesity. Curr Diabetes Rev 4 : 329–339.
3. LawsonHA, CheverudJM, WolfJB (2013) Genomic imprinting and parent-of-origin effects on complex traits. Nat Rev Genet 14 : 609–617.
4. GuilmatreA, SharpAJ (2012) Parent of origin effects. Clin Genet 81 : 201–209.
5. DongC, LiWD, GellerF, LeiL, LiD, et al. (2005) Possible genomic imprinting of three human obesity-related genetic loci. Am J Hum Genet 76 : 427–437.
6. LindsayRS, KobesS, KnowlerWC, BennettPH, HansonRL (2001) Genome-wide linkage analysis assessing parent-of-origin effects in the inheritance of type 2 diabetes and BMI in Pima Indians. Diabetes 50 : 2850–2857.
7. PatersonAD, PetronisA (1999) Sex-based linkage analysis of alcoholism. Genet Epidemiol 17 Suppl 1S289–294.
8. WyszynskiDF, PanhuysenCI (1999) Parental sex effect in families with alcoholism. Genet Epidemiol 17 Suppl 1S409–413.
9. StrauchK, FurstR, RuschendorfF, WindemuthC, DietterJ, et al. (2005) Linkage analysis of alcohol dependence using MOD scores. BMC Genet 6 Suppl 1S162.
10. SpeliotesEK, WillerCJ, BerndtSI, MondaKL, ThorleifssonG, et al. (2010) Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat Genet 42 : 937–948.
11. BarelO, ShalevSA, OfirR, CohenA, ZlotogoraJ, et al. (2008) Maternally inherited Birk Barel mental retardation dysmorphism syndrome caused by a mutation in the genomically imprinted potassium channel KCNK9. Am J Hum Genet 83 : 193–199.
12. QiL, MenzaghiC, SalveminiL, De BonisC, TrischittaV, et al. (2011) Novel locus FER is associated with serum HMW adiponectin levels. Diabetes 60 : 2197–2201.
13. JungJ, BarrettPQ, EckertGJ, EdenbergHJ, XueiX, et al. (2012) Variations in the potassium channel genes KCNK3 and KCNK9 in relation to blood pressure and aldosterone production: an exploratory study. J Clin Endocrinol Metab 97: E2160–2167.
14. PangDS, RobledoCJ, CarrDR, GentTC, VyssotskiAL, et al. (2009) An unexpected role for TASK-3 potassium channels in network oscillations with implications for sleep mechanisms and anesthetic action. Proc Natl Acad Sci U S A 106 : 17546–17551.
15. LindenAM, SanduC, AllerMI, VekovischevaOY, RosenbergPH, et al. (2007) TASK-3 knockout mice exhibit exaggerated nocturnal activity, impairments in cognitive functions, and reduced sensitivity to inhalation anesthetics. J Pharmacol Exp Ther 323 : 924–934.
16. LoweJK, MallerJB, Pe'erI, NealeBM, SalitJ, et al. (2009) Genome-wide association studies in an isolated founder population from the Pacific Island of Kosrae. PLoS Genet 5: e1000365.
17. JarickI, VogelCI, ScheragS, SchaferH, HebebrandJ, et al. (2011) Novel common copy number variation for early onset extreme obesity on chromosome 11q11 identified by a genome-wide analysis. Hum Mol Genet 20 : 840–852.
18. MorcosL, GeB, KokaV, LamKC, PokholokDK, et al. (2011) Genome-wide assessment of imprinted expression in human cells. Genome Biol 12: R25.
19. PollardKS, SerreD, WangX, TaoH, GrundbergE, et al. (2008) A genome-wide approach to identifying novel-imprinted genes. Hum Genet 122 : 625–634.
20. WermterAK, ScheragA, MeyreD, ReichwaldK, DurandE, et al. (2008) Preferential reciprocal transfer of paternal/maternal DLK1 alleles to obese children: first evidence of polar overdominance in humans. Eur J Hum Genet 16 : 1126–1134.
21. HeidIM, JacksonAU, RandallJC, WinklerTW, QiL, et al. (2010) Meta-analysis identifies 13 new loci associated with waist-hip ratio and reveals sexual dimorphism in the genetic basis of fat distribution. Nat Genet 42 : 949–960.
22. CuiY, LuQ, CheverudJM, LittellRC, WuR (2006) Model for mapping imprinted quantitative trait loci in an inbred F2 design. Genomics 87 : 543–551.
23. Yang J, Loos RJ, Powell JE, Medland SE, Speliotes EK, et al.. (2012) FTO genotype is associated with phenotypic variability of body mass index. Nature.
24. SunX, ElstonR, MorrisN, ZhuX (2013) What Is the Significance of Difference in Phenotypic Variability across SNP Genotypes? Am J Hum Genet 93 : 390–397.
25. ShenX, PetterssonM, RonnegardL, CarlborgO (2012) Inheritance beyond plain heritability: variance-controlling genes in Arabidopsis thaliana. PLoS Genet 8: e1002839.
26. ShibataK, DiatchenkoL, ZaykinDV (2009) Haplotype associations with quantitative traits in the presence of complex multilocus and heterogeneous effects. Genet Epidemiol 33 : 63–78.
27. GuoYF, ShenH, LiuYJ, WangW, XiongDH, et al. (2006) Assessment of genetic linkage and parent-of-origin effects on obesity. J Clin Endocrinol Metab 91 : 4001–4005.
28. Davey SmithG, SteerC, LearyS, NessA (2007) Is there an intrauterine influence on obesity? Evidence from parent child associations in the Avon Longitudinal Study of Parents and Children (ALSPAC). Arch Dis Child 92 : 876–880.
29. PatroB, LiberA, ZalewskiB, PostonL, SzajewskaH, et al. (2013) Maternal and paternal body mass index and offspring obesity: a systematic review. Ann Nutr Metab 63 : 32–41.
30. LinaberyAM, NahhasRW, JohnsonW, ChohAC, TowneB, et al. (2013) Stronger influence of maternal than paternal obesity on infant and early childhood body mass index: the Fels Longitudinal Study. Pediatr Obes 8 : 159–169.
31. GastwirthJL, GelYL, MiaoW (2009) The Impact of Levene's Test of Equality of Variances on Statistical Theory and Practice. Statistical Science 24 : 343–360.
32. RamseyPH (1994) Testing Variances in Psychological and Educational-Research. J Educ Stat 19 : 23–42.
33. GaoX, StarmerJ, MartinER (2008) A multiple testing correction method for genetic association studies using correlated single nucleotide polymorphisms. Genet Epidemiol 32 : 361–369.
34. HeF, ZhouJY, HuYQ, SunF, YangJ, et al. (2011) Detection of parent-of-origin effects for quantitative traits in complete and incomplete nuclear families with multiple children. Am J Epidemiol 174 : 226–233.
35. ZollnerS, PritchardJK (2007) Overcoming the winner's curse: estimating penetrance parameters from case-control data. Am J Hum Genet 80 : 605–615.
36. PrescottSM, LalouelJM, LeppertM (2008) From linkage maps to quantitative trait loci: the history and science of the Utah genetic reference project. Annu Rev Genomics Hum Genet 9 : 347–358.
37. Rio FrioT, CivicN, RansijnA, BeckmannJS, RivoltaC (2008) Two trans-acting eQTLs modulate the penetrance of PRPF31 mutations. Hum Mol Genet 17 : 3154–3165.
Štítky
Genetika Reprodukční medicína
Článek Comparative Phylogenomics Uncovers the Impact of Symbiotic Associations on Host Genome EvolutionČlánek Distribution and Medical Impact of Loss-of-Function Variants in the Finnish Founder PopulationČlánek Common Transcriptional Mechanisms for Visual Photoreceptor Cell Differentiation among PancrustaceansČlánek Integrative Genomics Reveals Novel Molecular Pathways and Gene Networks for Coronary Artery DiseaseČlánek An ARID Domain-Containing Protein within Nuclear Bodies Is Required for Sperm Cell Formation in
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2014 Číslo 7
-
Všechny články tohoto čísla
- Cuba: Exploring the History of Admixture and the Genetic Basis of Pigmentation Using Autosomal and Uniparental Markers
- Clonal Architecture of Secondary Acute Myeloid Leukemia Defined by Single-Cell Sequencing
- Mechanisms of Functional Variants That Impair Regulated Bicarbonate Permeation and Increase Risk for Pancreatitis but Not for Cystic Fibrosis
- Nucleosomes Shape DNA Polymorphism and Divergence
- Functional Diversification of Hsp40: Distinct J-Protein Functional Requirements for Two Prions Allow for Chaperone-Dependent Prion Selection
- Comparative Phylogenomics Uncovers the Impact of Symbiotic Associations on Host Genome Evolution
- Activation of the Immune System by Combinations of Common Alleles
- Age-Associated Sperm DNA Methylation Alterations: Possible Implications in Offspring Disease Susceptibility
- Muscle-Specific SIRT1 Gain-of-Function Increases Slow-Twitch Fibers and Ameliorates Pathophysiology in a Mouse Model of Duchenne Muscular Dystrophy
- MDRL lncRNA Regulates the Processing of miR-484 Primary Transcript by Targeting miR-361
- Hypersensitivity of Primordial Germ Cells to Compromised Replication-Associated DNA Repair Involves ATM-p53-p21 Signaling
- Intrapopulation Genome Size Variation in Reflects Life History Variation and Plasticity
- SlmA Antagonism of FtsZ Assembly Employs a Two-pronged Mechanism like MinCD
- Distribution and Medical Impact of Loss-of-Function Variants in the Finnish Founder Population
- Determinative Developmental Cell Lineages Are Robust to Cell Deaths
- DELLA Protein Degradation Is Controlled by a Type-One Protein Phosphatase, TOPP4
- Wnt Signaling Interacts with Bmp and Edn1 to Regulate Dorsal-Ventral Patterning and Growth of the Craniofacial Skeleton
- Common Transcriptional Mechanisms for Visual Photoreceptor Cell Differentiation among Pancrustaceans
- UVB Induces a Genome-Wide Acting Negative Regulatory Mechanism That Operates at the Level of Transcription Initiation in Human Cells
- The Nesprin Family Member ANC-1 Regulates Synapse Formation and Axon Termination by Functioning in a Pathway with RPM-1 and β-Catenin
- Combinatorial Interactions Are Required for the Efficient Recruitment of Pho Repressive Complex (PhoRC) to Polycomb Response Elements
- Recombination in the Human Pseudoautosomal Region PAR1
- Microsatellite Interruptions Stabilize Primate Genomes and Exist as Population-Specific Single Nucleotide Polymorphisms within Individual Human Genomes
- An Intronic microRNA Links Rb/E2F and EGFR Signaling
- An Essential Nonredundant Role for Mycobacterial DnaK in Native Protein Folding
- Integrative Genomics Reveals Novel Molecular Pathways and Gene Networks for Coronary Artery Disease
- The Genomic Landscape of the Ewing Sarcoma Family of Tumors Reveals Recurrent Mutation
- Evolution and Genetic Architecture of Chromatin Accessibility and Function in Yeast
- An ARID Domain-Containing Protein within Nuclear Bodies Is Required for Sperm Cell Formation in
- Stage-Dependent and Locus-Specific Role of Histone Demethylase Jumonji D3 (JMJD3) in the Embryonic Stages of Lung Development
- Genome Wide Association Identifies Common Variants at the Locus Influencing Plasma Cortisol and Corticosteroid Binding Globulin
- Regulation of Feto-Maternal Barrier by Matriptase- and PAR-2-Mediated Signaling Is Required for Placental Morphogenesis and Mouse Embryonic Survival
- Apomictic and Sexual Germline Development Differ with Respect to Cell Cycle, Transcriptional, Hormonal and Epigenetic Regulation
- Functional EF-Hands in Neuronal Calcium Sensor GCAP2 Determine Its Phosphorylation State and Subcellular Distribution , and Are Essential for Photoreceptor Cell Integrity
- Comparison of Methods to Account for Relatedness in Genome-Wide Association Studies with Family-Based Data
- Knock-In Reporter Mice Demonstrate that DNA Repair by Non-homologous End Joining Declines with Age
- Cis and Trans Effects of Human Genomic Variants on Gene Expression
- 8.2% of the Human Genome Is Constrained: Variation in Rates of Turnover across Functional Element Classes in the Human Lineage
- Novel Approach Identifies SNPs in and with Evidence for Parent-of-Origin Effect on Body Mass Index
- Hypoxia Adaptations in the Grey Wolf () from Qinghai-Tibet Plateau
- A Loss of Function Screen of Identified Genome-Wide Association Study Loci Reveals New Genes Controlling Hematopoiesis
- Unraveling Genetic Modifiers in the Mouse Model of Absence Epilepsy
- DNA Topoisomerase 1α Promotes Transcriptional Silencing of Transposable Elements through DNA Methylation and Histone Lysine 9 Dimethylation in
- The Coding and Noncoding Architecture of the Genome
- A Novel Locus Is Associated with Large Artery Atherosclerotic Stroke Using a Genome-Wide Age-at-Onset Informed Approach
- Brg1 Loss Attenuates Aberrant Wnt-Signalling and Prevents Wnt-Dependent Tumourigenesis in the Murine Small Intestine
- The PTK7-Related Transmembrane Proteins Off-track and Off-track 2 Are Co-receptors for Wnt2 Required for Male Fertility
- The Co-factor of LIM Domains (CLIM/LDB/NLI) Maintains Basal Mammary Epithelial Stem Cells and Promotes Breast Tumorigenesis
- Essential Genetic Interactors of Required for Spatial Sequestration and Asymmetrical Inheritance of Protein Aggregates
- Meiosis-Specific Cohesin Component, Is Essential for Maintaining Centromere Chromatid Cohesion, and Required for DNA Repair and Synapsis between Homologous Chromosomes
- Silencing Is Noisy: Population and Cell Level Noise in Telomere-Adjacent Genes Is Dependent on Telomere Position and Sir2
- The Two Cis-Acting Sites, and , Contribute to the Longitudinal Organisation of Chromosome I
- A Broadly Conserved G-Protein-Coupled Receptor Kinase Phosphorylation Mechanism Controls Smoothened Activity
- Requirements for Acute Burn and Chronic Surgical Wound Infection
- LIN-42, the PERIOD homolog, Negatively Regulates MicroRNA Transcription
- WAPL Is Essential for the Prophase Removal of Cohesin during Meiosis
- Expression in Planarian Neoblasts after Injury Controls Anterior Pole Regeneration
- Sox11 Is Required to Maintain Proper Levels of Hedgehog Signaling during Vertebrate Ocular Morphogenesis
- Accumulation of a Threonine Biosynthetic Intermediate Attenuates General Amino Acid Control by Accelerating Degradation of Gcn4 via Pho85 and Cdk8
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- Wnt Signaling Interacts with Bmp and Edn1 to Regulate Dorsal-Ventral Patterning and Growth of the Craniofacial Skeleton
- Novel Approach Identifies SNPs in and with Evidence for Parent-of-Origin Effect on Body Mass Index
- Hypoxia Adaptations in the Grey Wolf () from Qinghai-Tibet Plateau
- DNA Topoisomerase 1α Promotes Transcriptional Silencing of Transposable Elements through DNA Methylation and Histone Lysine 9 Dimethylation in
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Současné možnosti léčby obezity
nový kurzAutoři: MUDr. Martin Hrubý
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání
















