Individual Participant Data (IPD) Meta-analyses of Diagnostic and Prognostic Modeling Studies: Guidance on Their Use
article has not abstract
Published in the journal:
. PLoS Med 12(10): e32767. doi:10.1371/journal.pmed.1001886
Category:
Guidelines and Guidance
doi:
https://doi.org/10.1371/journal.pmed.1001886
Summary
article has not abstract
Summary Points
Individual participant data meta-analyses (IPD-MAs) provide unique opportunities not only for therapeutic studies but also for diagnostic and prognostic prediction modeling studies.
IPD-MAs of prediction modeling studies allow for more robust development of prediction models, as well as for directly validating them and testing their generalizability across different (sub)populations and settings.
Methods for IPD-MA of prediction modeling studies fundamentally differ from other types of IPD-MA research, because of the focus on the estimation of absolute risks and the importance of covariates.
When heterogeneity is present in an IPD-MA of prediction models, special care is needed to enable tailoring of the prediction model to (sub)populations or settings at hand, to enhance their generalizability and usefulness.
Introduction
A fundamental part of medical research is the development and validation of diagnostic and prognostic prediction models [1,2]. These prediction models aim to predict the absolute probability that a certain disease or condition is currently present (diagnostic models) or that an outcome will occur within a specific follow-up period (prognostic models) for an individual subject.
Prediction models typically rely on multiple predictors, which can include demographic characteristics, medical history and physical examination items, or more complex measurements from, for example, medical imaging, electrophysiology, pathology, and biomarkers. Also for diagnostic models, estimates of probabilities are rarely based on a single test, and doctors naturally integrate several patient characteristics and symptoms [3]. A broad range of prediction modeling techniques exist, like regression approaches, neural network models, decision tree models, genetic programming models, and support vector machine learning models, although prediction models developed by a multivariable regression approach are by far prevailing.
It is widely recommended that a developed prediction model should not be used in practice before being externally validated—at least once—in other individuals than those used for model development [4–7]. Unfortunately, most prediction models are poorly or not at all validated, rendering interpretation of their generalizability difficult. In addition, many systematic reviews showed that for the same outcome or same target population, numerous competing models exist [8–10]. Generally speaking, researchers often ignore existing prediction models and develop yet another prediction model from their own data [2]. This practice sustains a cycle of underpowered prediction model development studies and poor knowledge about the generalizability and applicability of developed prediction models. Evidence synthesis and meta-analysis of individual participant data (IPD) from multiple studies seems to be a unique opportunity to address these problems, as it allows researchers to develop and directly validate models on large datasets and across a wide range of populations and settings, to directly test a model’s generalizability (Fig 1) [11–13].
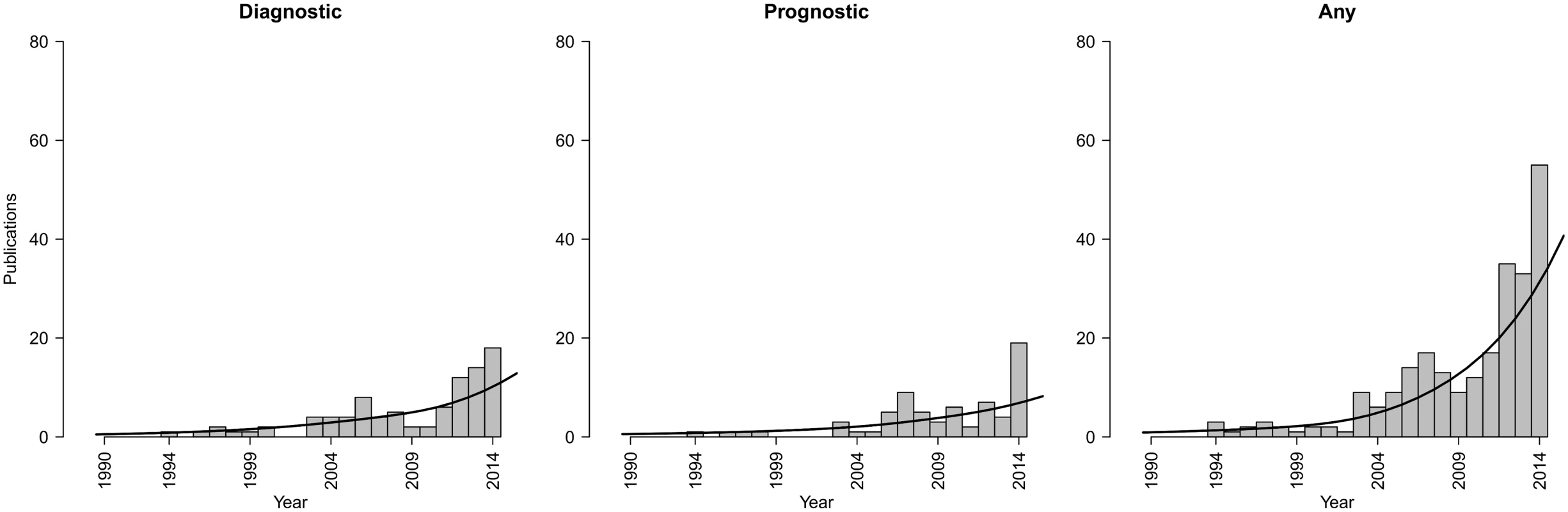
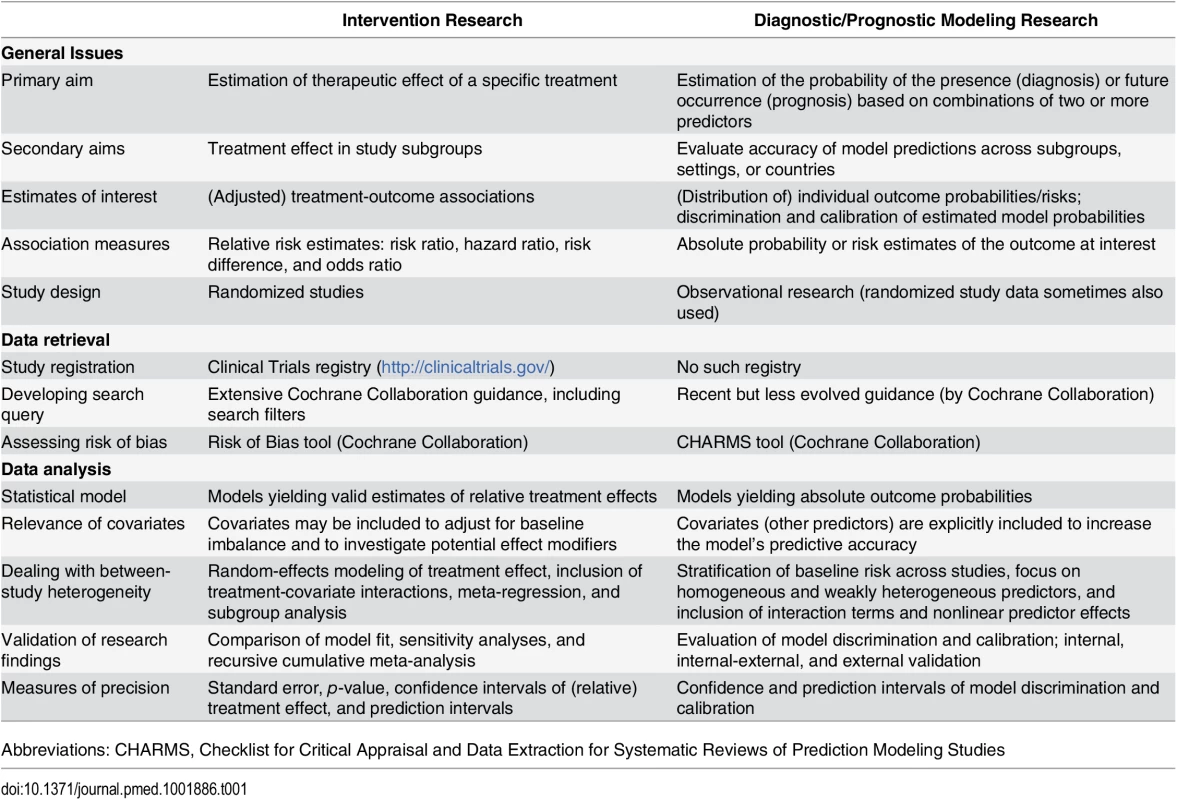
There is currently little guidance on how to conduct an IPD meta-analysis (IPD-MA) for developing and/or validating diagnostic or prognostic prediction models [15]. To date, most IPD-MA articles focus on estimating relative quantities, like a risk ratio, hazard ratio, or odds ratio for a specific treatment or a specific etiologic factor. In contrast, prediction modeling research is focused on developing and validating multivariable models aimed at calculating an absolute risk estimate of the combined variables, rather than estimating the relative effect of a specific treatment or etiologic factor. Furthermore, prediction modeling studies focus entirely on the role and joint contribution of multiple covariates, whereas intervention studies in principle rely on randomization to reduce the role of covariates (Table 1). Hence, IPD-MAs of randomized intervention and etiological studies, which are beyond the scope of this paper and are instead addressed in the accompanying paper [16], differ from IPD-MAs of multivariable prediction models, which are the focus of this paper.
We provide an overview of the advantages and limitations of IPD-MAs aiming to develop a novel prediction model or to validate one or more existing models across multiple datasets. This overview is based on published guidelines and existing recommendations for the conduct of prediction modeling studies and of IPD-MA research. We illustrate this overview with examples of recently published IPD-MAs of prediction models across various medical domains. Our aim is to help researchers, readers, reviewers, and editors to identify and understand the key issues involved with such IPD-MA projects.
Types of IPD-MA of Prediction Modeling Studies
Several types of IPD-MA can be distinguished. When a single (previously published) prediction model is available, typical research aims include the following:
To validate and summarize the model’s performance across various study populations, settings, and domains. For example, Geersing and colleagues used an IPD-MA to examine the predictive accuracy of the Wells rule for diagnosing deep vein thrombosis (DVT) across different subgroups of suspected patients [17].
To tailor (update) the model to specific populations or settings. For instance, Majed and colleagues evaluated whether the calibration of the Framingham risk equation for coronary heart disease and stroke improved by applying local adjustments [18].
To examine the added value of a specific predictor or (bio)marker to the model across different study populations, settings, and domains. For example, an IPD-MA was performed to summarize the added value of common carotid intima-media thickness (CIMT) in 10-year risk prediction of first-time myocardial infarctions or strokes in the general population, above that of the Framingham Risk Score [19].
When various competing prediction models are available that were developed for the same target population or the same outcome across various study populations, typical research aims of an IPD-MA include the following:
To compare the models’ performance across various study populations, settings, and domains. For instance, an IPD-MA was used to validate and compare all noninvasive risk scores for the prediction of developing type 2 diabetes in individuals of the general population [20].
To combine the most promising models and adjust them to specific study populations, settings, and domains. This approach is illustrated by Debray and colleagues, who validated and updated all existing diagnostic models for predicting the presence of DVT across different settings and proceeded to combine them into a single meta-model [21].
Finally, when no prediction models are available, an IPD-MA can be used to develop and directly validate a new prediction model using the IPD from all relevant studies. An example is the development of the prognostic PHASES score for prediction of risk of rupture of intracranial aneurysms in patients with aneurysms but without any treatment [22].
Advantages and Challenges of an IPD-MA in Prediction Research
Box 1 summarizes the general advantages and challenges of IPD-MA in prediction studies. An IPD-MA of prediction models has a major advantage not only in developing more robust prediction models because of the increased sample size but also in directly validating the models and hence revealing their clinical usefulness. This combination of development, validation, and testing for usefulness can be applied across different patient subgroups, different target populations, and even different care settings, if such datasets are included in the IPD-MA. Whereas a single prediction modelling study is usually confined to quantifying the average predictive performance of the prediction model across the entire study population, an IPD-MA allows for quantifying subgroup- or setting-specific performances, and the prediction model can even be tailored to optimize its performance in these specific (sub)groups or settings. For example, Geersing and colleagues examined the diagnostic accuracy of the Wells prediction rule for diagnosing DVT across different subgroups of suspected patients and evaluated whether the rule had to be tailored to enhance its accuracy in these subgroups [17]. Table 2 highlights unique advantages of IPD access for different research aims.
Box 1. Advantages and Challenges of IPD-MA of Multivariable Prediction Modeling Studies, Based on Ahmed and colleagues [15]
Advantages
Increases the total sample size. This reduces the risk of incidental findings, increases the precision of study results, and enables the development of more robust prediction models.
Increases the available case-mix variability. This enhances the potential generalizability of prediction models across subgroups, settings, and countries.
Ability to standardize analysis methods across IPD sets. For example, one can standardize the type of statistical model used (such as Cox, logistic or other model), the predictor and outcome definitions, and the methods to account for differences in censoring and in lengths of follow-up.
Ability to investigate more complex associations, such as nonlinearity of predictor effects, predictor interactions, and time-varying predictor effects.
Ability to explore heterogeneity in the predictive performance of the models—for example, in whom (in which subgroups, countries, or settings) or under which circumstances does a prediction model not perform adequately.
Ability to evaluate generalizability and thus usability of prediction models across different situations.
Challenges
Unavailability of IPD in some studies and assessing the impact of their absence on predictive performance of a developed or validated prediction model.
Methodological quality assessment of primary prediction modeling studies is yet less well developed.
Dealing with different definitions of predictors and outcomes; with different data sources (such as prospective and retrospective cohort studies, case-control studies, case-cohort studies, or randomized trials); and with different (or outdated) treatment strategies, especially when older and newer primary studies are combined.
Dealing with missing data, including partially missing predictors and outcome data, as well as completely missing predictors in some studies.
Dealing with heterogeneity in predictor effects and outcome occurrence across the included primary studies.

Ahmed and colleagues recently provided over 20 recommendations to improve the development and validation of prediction models using IPD from multiple studies [15]. We here elaborate on five key aspects of IPD-MA of prediction models: prespecifying the IPD-MA, identifying the relevant studies for the IPD-MA, assessment of risk of bias of individual studies/datasets, implementation of appropriate statistical methods, and reporting of results.
Prespecifying the IPD-MA
It is important for IPD-MA projects that one a priori defines the rationale, methods, conduct, and analyses of the IPD-MA [23]. When IPD-MA projects are based on a systematic review, the protocol should also indicate which type of publications are deemed relevant. Researchers may, for instance, seek all publications that have already developed or validated a prediction model for a specific target population, specific setting, or for specific outcome(s) [24–26]. Alternatively, researchers may seek all publications that used a dataset that fit the IPD-MA objective. Study protocols are certainly relevant for IPD-MAs that are prospectively planned and should ideally be accessible for inspection by external parties [23,27,28]. By setting common quality standards and standardizing predictor definitions, measurement methods, and outcome recoding, the consistency across included datasets increases, thereby reducing the risk of bias. Study protocols may also help to convince other researchers to participate in the IPD-MA and to share their IPD. Examples of relevant databases for protocols of systematic reviews are the Cochrane Library (www.thecochranelibrary.com) and the International Prospective Register of Systematic Reviews (www.crd.york.ac.uk/prospero/).
Identifying the Relevant Studies for the IPD-MA
Various competing strategies can be initiated for collecting the relevant studies in an IPD-MA [15]. Similar to meta-analyses of randomized trials of treatments [16,29,30], these studies should ideally be identified through a systematic review. However, it is also possible to prospectively set up a collaborative group of selected researchers active on the same topic who agree to share their IPD. Examples of such collaborations are the European Prospective Investigation into Cancer and Nutrition (N > 520,000 from ten European countries) [31] and the Emerging Risk Factors Collaboration (N > 2.2 million participants in 125 prospective studies) [32]. Furthermore, if there are known relevant studies that did not provide their IPD, it may help to extract their summary information. Examples of such information are measures of model performance including c-statistic and calibration slopes with their 95% confidence intervals and estimated predictor effects. Recently, methods have been developed to combine such summary estimates with the results from the IPD-MA [21,33,34].
Assessing Risk of Bias of Included Studies
Similar to any type of systematic review, the quality of an IPD-MA of prediction models strongly depends upon the methodological quality of included studies. When these studies have flaws in the design, conduct, or analysis, the IPD-MA may yield biased estimates of predictive performance. Researchers should therefore evaluate the methodological quality in each of the included prediction model studies. The CHARMS checklist is a very recent guideline and checklist for data extraction and critical appraisal of primary prediction model studies in systematic reviews [35]. This checklist may also be used for critically appraising the primary prediction modeling studies to be included in the IPD-MA. Progress on a formal risk-of-bias tool for prediction modeling studies, developed by various authors around the globe, including co-conveners of the Cochrane Prognosis Methods Group, is underway (www.systematic-reviews.com/probast/).
Statistical Methods
The statistical analysis approach of an IPD-MA of prediction models has to deal with several key issues. We here elaborate on missing data and between-study heterogeneity. Another key issue is the combination of IPD and aggregate data from the literature (Table 2). Combining IPD and aggregate data for the development and validation of multivariable prediction models is, however, not straightforward and therefore beyond the scope of this paper. Statistical methods for this purpose have previously been described [21,33,34,36].
Missing Data
Missing data basically appear when subject characteristics have not fully been recorded within the primary studies or were measured inconsistently across studies (for example, a predictor that was measured on a continuous versus categorical scale), so-called partial missing data. Missing data may also arise when some of the included studies did not measure a certain predictor at all, the so-called systematically missing predictors [37–39]. In any case, it is increasingly acknowledged that missing data should be addressed using multiple imputation techniques; this should also be done in IPD-MAs. These techniques generate (multiple) completed versions of each original dataset. For partial missing data, imputation can be applied separately for each study of the IPD-MA to allow for heterogeneity in associations between observed and missing predictors. However, when there is a mixture of partial and systematically missing data, more advanced imputation techniques are needed to simultaneously impute the IPD from each study in the IPD-MA [37,38].
Between-Study Heterogeneity
Between-study heterogeneity arises when the studies of an IPD-MA yield substantially different estimates of model performance (for example, when validating an existing prediction model), of a predictor’s added predictive value (for example, when examining the added value of a certain predictor to an existing prediction model), or of certain predictor effects (for example, when developing a novel prediction model). Researchers should therefore investigate the presence of heterogeneity across the available studies and check whether its extent can be reduced or explained. As a first step, researchers may compare the characteristics of included studies and populations. Depending on the research aim of the IPD-MA, different methods can then be applied to account for the presence of between-study heterogeneity.
When externally validating one or more prediction models in an IPD-MA, it is recommended to investigate the influence of specific study characteristics such as case-mix differences on the predictive performance of the models [40,41]. This could reveal under which circumstances the model remains valid and how the model may be improved upon for different subgroups or settings. The presence of between-study heterogeneity in model performance can be investigated using traditional (random effects) techniques that are sometimes used in the analysis of multinational or multicenter randomized trials. For instance, Kengne and colleagues validated all existing models for predicting the development of type 2 diabetes in the general population, separately in different countries, and then pooled the resulting performance estimates using a traditional random effects model [20]. When such random effects analysis conveys substantial heterogeneity in the performance of a prediction model in a certain country, (sub)population, or setting, an IPD-MA allows one to tailor or update the prediction model to enhance its performance in that specific country, subpopulation, or setting. An example is the validation and updating of the sex-specific Framingham risk equation for coronary heart disease and stroke [18]. An IPD-MA was used to adjust this model for the baseline survival and mean predictor values of each included country and to re-estimate country-specific predictor effects. The study concluded that the updated model, despite yielding poor discrimination, achieved better calibration in a European population of middle-aged men.
When investigating the added value of a specific (new) predictor to existing predictors, it is recommended to verify whether this added predictive value substantially varies across the included studies of an IPD-MA and, if so, to evaluate under which circumstances and in which types of individuals or settings it can be used as an addition to existing predictors or models. For example, Den Ruijter and colleagues tested heterogeneity in the added value of CIMT above that of the Framingham Risk Score by exploring the presence of interaction between cohort membership and CIMT [19]. Because no evidence for heterogeneity was found and because the improvement in 10-year risk prediction of first-time myocardial infarction or stroke was small, they concluded that the addition of CIMT on top of Framingham Risk Score is unlikely to be of clinical importance.
When developing a novel prediction model from an IPD-MA, researchers may quantify the degree of variation in outcome frequency and in predictor effects across the IPD-MA studies using traditional meta-analysis methods [11]. This information could then be used to decide which and how predictors will be included during the statistical analyses. It has been demonstrated that using average predictor effects (for instance, as obtained from random effects models) is detrimental when their association substantially varies across studies [11]. For this reason, efforts should be made to facilitate tailoring of the model to new study populations. This can, for instance, be achieved by applying stratification, by omitting predictors with heterogeneous effects, or by considering nonlinear terms and interaction effects. In contrast to prediction models developed from a single dataset, an IPD-MA has the unique feature of directly applying internal-external cross validation of a developed model [11,13,42]. This method iteratively discards one study of the IPD-MA for external validation purposes and uses the remaining studies for the model development. This directly allows one to investigate whether a developed model predicts differently across certain populations, settings, or even subgroups and whether the model would differ in fit for purpose when applied in practice. Also, it is an ideal method to deal with between-study heterogeneity to determine the extent of the generalizability and thus applicability of the developed model. Finally, when the calibration and discrimination performance measures from an internal-external cross validation are pooled using a multivariate meta-analysis approach [40], it is even possible to evaluate whether a prediction model’s average performance varies across different subgroups, populations, or settings. This in turn helps to identify under what circumstances in clinical practice the model can reliably be used and when and whether a developed model first requires tailoring to specific clinical situations to enhance its usefulness for the situation at hand.
Reporting IPD-MA of Prediction Modeling Studies
Similar to meta-analysis of randomized trials of interventions [43], IPD-MA should be reported fully and transparently as well, to allow readers to assess the strengths and weaknesses of the investigation. Although specific guidelines are currently lacking, important issues to report should clearly include details on study identification, study inclusion and exclusion criteria, predictor and outcome definitions, the amount of missing subject-level and missing study-level data, the presence of between-study heterogeneity, and how this is dealt with [15]. Furthermore, to address potential concerns over selective nonpublication, authors should explain whether analyses could be completed as planned or why they had to be revised. Further—but less specific—guidance can be found in the recent Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA)-IPD reporting statement [44] and in the very recent Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD) reporting guideline for studies on developing, validating, or updating a prediction model [3,45].
Conclusions
Systematic review and meta-analysis of IPD is widely recognized as a gold standard approach in intervention research and is equally pivotal in prediction modeling research. Having IPD from multiple studies is particularly useful for improving the performance of novel prediction models across different study populations, settings, and domains and to attain a better understanding of the generalizability of prediction models. It is, however, important to acknowledge that IPD-MAs are no panacea against poorly conceived and conducted primary studies. Well-designed prospective studies remain paramount and could, for instance, benefit by involving multiple centers or countries and applying IPD-MA methodology. Prospective studies are also needed for evaluating the impact of prediction models on decision making and patient outcomes. The guidance provided in this article may help researchers to decide upon appropriate strategies when conducting an IPD-MA in prediction modeling research and assist readers, reviewers, and practitioners when evaluating the quality of resulting evidence.
Zdroje
1. Moons KGM, Royston P, Vergouwe Y, Grobbee DE, Altman DG (2009) Prognosis and prognostic research: what, why, and how? British Medical Journal 338: b375. doi: 10.1136/bmj.b375 19237405
2. Steyerberg EW, Moons KGM, van der Windt DA, Hayden JA, Perel P, et al. (2013) Prognosis research strategy (PROGRESS) 3: Prognostic model research. PLoS Medicine 10: e1001381. doi: 10.1371/journal.pmed.1001381 23393430
3. Collins GS, Reitsma JB, Altman DG, Moons KGM (2015) Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. Annals of Internal Medicine 162: 55–63. doi: 10.7326/M14-0697 25560714
4. Moons KGM, Kengne AP, Grobbee DE, Royston P, Vergouwe Y, et al. (2012) Risk prediction models: II. External validation, model updating, and impact assessment. Heart 98: 691–698. doi: 10.1136/heartjnl-2011-301247 22397946
5. Altman DG, Vergouwe Y, Royston P, Moons KGM (2009) Prognosis and prognostic research: validating a prognostic model. British Medical Journal 338: b605. doi: 10.1136/bmj.b605 19477892
6. Steyerberg EW (2009) Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. Statistics for Biology and Health. New York: Springer.
7. Harrell FE Jr (2001) Regression Modeling Strategies with applications to Linear Models, Logistic Regression and Survival Analysis. Springer Series in Statistics. New York: Springer.
8. Collins GS, Mallett S, Omar O, Yu LM (2011) Developing risk prediction models for type 2 diabetes: a systematic review of methodology and reporting. BMC Medicine 9: 103. doi: 10.1186/1741-7015-9-103 21902820
9. Altman DG (2009) Prognostic models: a methodological framework and review of models for breast cancer. Cancer Investigation 27: 235–243. doi: 10.1080/07357900802572110 19291527
10. Perel P, Edwards P, Wentz R, Roberts I (2006) Systematic review of prognostic models in traumatic brain injury. BMC Medical Informatics and Decision Making 6: 38. 17105661
11. Debray TPA, Moons KGM, Ahmed I, Koffijberg H, Riley RD (2013) A framework for developing, implementing, and evaluating clinical prediction models in an individual participant data meta-analysis. Statistics in Medicine 32: 3158–3180. doi: 10.1002/sim.5732 23307585
12. Cai T, Gerds TA, Zheng Y, Chen J (2011) Robust prediction of t-year survival with data from multiple studies. Biometrics 67: 436–444. doi: 10.1111/j.1541-0420.2010.01462.x 20670303
13. Royston P, Parmar MKB, Sylvester R (2004) Construction and validation of a prognostic model across several studies, with an application in superficial bladder cancer. Statistics in Medicine 23: 907–926. 15027080
14. Riley RD, Simmonds MC, Look MP (2007) Evidence synthesis combining individual patient data and aggregate data: a systematic review identified current practice and possible methods. Journal of Clinical Epidemiology 60: 431–439. 17419953
15. Ahmed I, Debray TPA, Moons KGM, Riley RD (2014) Developing and validating risk prediction models in an individual participant data meta-analysis. BMC Medical Research Methodology 14: 3. doi: 10.1186/1471-2288-14-3 24397587
16. Tierney J, Vale C, Riley R, Tudur Smith C, Stewart L, et al. (2015) Individual participant data (IPD) meta-analyses of randomised controlled trials: Guidance on their use. PLoS Medicine 12: e1001855. doi: 10.1371/journal.pmed.1001855 26196287
17. Geersing GJ, Zuithoff NPA, Kearon C, Anderson DR, Ten Cate-Hoek AJ, et al. (2014) Exclusion of deep vein thrombosis using the wells-rule in clinically important subgroups: Individual patient data meta-analysis. British Medical Journal 348: g1340. doi: 10.1136/bmj.g1340 24615063
18. Majed B, Tafflet M, Kee F, Haas B, Ferrieres J, et al. (2013) External validation of the 2008 Framingham cardiovascular risk equation for CHD and stroke events in a European population of middle-aged men. the PRIME study. Preventive Medicine 57: 49–54. doi: 10.1016/j.ypmed.2013.04.003 23603213
19. Den Ruijter HM, Peters SAE, Anderson TJ, Britton AR, Dekker JM, et al. (2012) Common carotid intima-media thickness measurements in cardiovascular risk prediction: a meta-analysis. The Journal of the American Medical Association 308: 796–803. doi: 10.1001/jama.2012.9630 22910757
20. Kengne AP, Beulens JWJ, Peelen LM, Moons KGM, van der Schouw YT, et al. (2014) Non-invasive risk scores for prediction of type 2 diabetes (EPIC-InterAct): a validation of existing models. The Lancet Diabetes & Endocrinology 2: 19–29. doi: 10.1016/S2213-8587(13)70103-7 24622666
21. Debray TPA, Koffijberg H, Nieboer D, Vergouwe Y, Steyerberg EW, et al. (2014) Meta-analysis and aggregation of multiple published prediction models. Statistics in Medicine 33: 2341–2362. doi: 10.1002/sim.6080 24752993
22. Greving JP, Wermer MJH, Brown RDJ, Morita A, Juvela S, et al. (2014) Development of the PHASES score for prediction of risk of rupture of intracranial aneurysms: a pooled analysis of six prospective cohort studies. Lancet Neurology 13: 59–66. doi: 10.1016/S1474-4422(13)70263-1 24290159
23. Peat G, Riley RD, Croft P, Morley KI, Kyzas PA, et al. (2014) Improving the transparency of prognosis research: the role of reporting, data sharing, registration, and protocols. PLoS Medicine 11: e1001671. doi: 10.1371/journal.pmed.1001671 25003600
24. Geersing GJ, Bouwmeester W, Zuithoff P, Spijker R, Leeflang M, et al. (2012) Search filters for finding prognostic and diagnostic prediction studies in medline to enhance systematic reviews. PLoS ONE 7: e32844. doi: 10.1371/journal.pone.0032844 22393453
25. Wilczynski NL, Haynes RB, the Hedges Team (2004) Developing optimal search strategies for detecting clinically sound prognostic studies in MEDLINE: an analytic survey. BMC Medical Research Methodology 2: 23. doi: 10.1186/1741-7015-2-23 15189561
26. Ingui BJ, Rogers MA (2001) Searching for clinical prediction rules in MEDLINE. Journal of the American Medical Informatics Association 8: 391–397. doi: 10.1136/jamia.2001.0080391 11418546
27. Debray TPA, Moons KGM, Abo-Zaid GMA, Koffijberg H, Riley RD (2013) Individual participant data meta-analysis for a binary outcome: one-stage or two-stage? PLoS ONE 8: e60650. doi: 10.1371/journal.pone.0060650 23585842
28. Blettner M, Sauerbrei W, Schlehofer B, Scheuchenpflug T, Friedenreich C (1999) Traditional reviews, meta-analyses and pooled analyses in epidemiology. International Journal of Epidemiology 28: 1–9. 10195657
29. Tudur Smith C, Dwan K, Altman DG, Clarke M, Riley R, et al. (2014) Sharing individual participant data from clinical trials: an opinion survey regarding the establishment of a central repository. PLoS ONE 9: e97886. doi: 10.1371/journal.pone.0097886 24874700
30. Clarke MJ, Stewart LA (1997) Meta-analyses using individual patient data. Journal of Evaluation in Clinical Practice 3: 207–212. 9406108
31. Riboli E, Hunt KJ, Slimani N, Ferrari P, Norat T, et al. (2002) European prospective investigation into cancer and nutrition (EPIC): study populations and data collection. Public Health Nutrition 5: 1113–1124. doi: 10.1079/PHN2002394 12639222
32. The Emerging Risk Factors Collaboration (2007) The emerging risk factors collaboration: analysis of individual data on lipid, inflammatory and other markers in over 1.1 million participants in 104 prospective studies of cardiovascular diseases. European Journal of Epidemiology 22: 839–869. 17876711
33. Debray TPA, Koffijberg H, Lu D, Vergouwe Y, Steyerberg EW, et al. (2012) Incorporating published univariable associations in diagnostic and prognostic modeling. BMC Medical Research Methodology 12: 121. doi: 10.1186/1471-2288-12-121 22883206
34. Debray TPA, Koffijberg H, Vergouwe Y, Moons KG, Steyerberg EW (2012) Aggregating published prediction models with individual participant data: a comparison of different approaches. Statistics in Medicine 31: 2697–2712. doi: 10.1002/sim.5412 22733546
35. Moons KGM, de Groot JAH, Bouwmeester W, Vergouwe Y, Mallett S, et al. (2014) Critical appraisal and data extraction for systematic reviews of clinical prediction modelling studies: The CHARMS checklist. PLoS Medicine 11: e1001744. doi: 10.1371/journal.pmed.1001744 25314315
36. Steyerberg EW, Eijkemans MJ, Van Houwelingen JC, Lee KL, Habbema JD (2000) Prognostic models based on literature and individual patient data in logistic regression analysis. Statistics in Medicine 19: 141–160. doi: 10.1002/(SICI)1097-0258(20000130)19:2<141::AID-SIM334>3.0.CO;2-O 10641021
37. Jolani S, Debray TPA, Koffijberg H, van Buuren S, Moons KGM (2015) Imputation of systematically missing predictors in an individual participant data meta-analysis: a generalized approach using MICE. Statistics in Medicine 34: 1841–1863. doi: 10.1002/sim.6451 25663182
38. Resche-Rigon M, White IR, Bartlett JW, Peters SAE, Thompson SG (2013) Multiple imputation for handling systematically missing confounders in meta-analysis of individual participant data. Statistics in Medicine 32: 4890–4905. doi: 10.1002/sim.5894 23857554
39. The Fibrinogen Studies Collaboration (2009) Systematically missing confounders in individual participant data meta-analysis of observational cohort studies. Statistics in Medicine 28: 1218–1237. doi: 10.1002/sim.3540 19222087
40. Snell K, Hui H, Debray T, Ensor J, Look M, et al. (2015) Multivariate meta-analysis of individual participant data helped externally validate the performance and implementation of a prediction model. Journal of Clinical Epidemiology. E-pub ahead of print. doi: 10.1016/j.jclinepi.2015.05.009
41. Debray TPA, Vergouwe Y, Koffijberg H, Nieboer D, Steyerberg EW, et al. (2015) A new framework to enhance the interpretation of external validation studies of clinical prediction models. Journal of Clinical Epidemiology 68: 279–289. doi: 10.1016/j.jclinepi.2014.06.018 25179855
42. Steyerberg EW, Harrell FEJ (2015) Prediction models need appropriate internal, internal-external, and external validation. Journal of Clinical Epidemiology. E-pub ahead of print. doi: 10.1016/j.jclinepi.2015.04.005
43. Liberati A, Altman DG, Tetzlaff J, Mulrow C, Gøtzsche PC, et al. (2009) The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate healthcare interventions: explanation and elaboration. British Medical Journal 339: b2700. doi: 10.1136/bmj.b2700 19622552
44. Stewart LA, Clarke M, Rovers M, Riley RD, Simmonds M, et al. (2015) Preferred reporting items for a systematic review and meta-analysis of individual participant data: The PRISMA-IPD statement. Journal of the American Medical Association 313: 1657–1665. doi: 10.1001/jama.2015.3656 25919529
45. Moons KGM, Altman DG, Reitsma JB, Ioannidis JPA, Macaskill P, et al. (2015) Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): Explanation and elaboration. Annals of Internal Medicine 162: W1–W73. doi: 10.7326/M14-0698 25560730
Štítky
Interní lékařstvíČlánek vyšel v časopise
PLOS Medicine
2015 Číslo 10
- Příznivý vliv Armolipidu Plus na hladinu cholesterolu a zánětlivé parametry u pacientů s chronickým subklinickým zánětem
- Berberin: přírodní hypolipidemikum se slibnými výsledky
- Léčba bolesti u seniorů
- Flexofytol® – přírodní revoluce v boji proti osteoartróze kloubů
- Nutraceutikum Armolipid Plus podle klinických důkazů zlepšuje lipidový profil − metaanalýza
Nejčtenější v tomto čísle
- Effect of Health Risk Assessment and Counselling on Health Behaviour and Survival in Older People: A Pragmatic Randomised Trial
- Using Qualitative Evidence in Decision Making for Health and Social Interventions: An Approach to Assess Confidence in Findings from Qualitative Evidence Syntheses (GRADE-CERQual)
- Monitoring Pharmacologically Induced Immunosuppression by Immune Repertoire Sequencing to Detect Acute Allograft Rejection in Heart Transplant Patients: A Proof-of-Concept Diagnostic Accuracy Study
- The REporting of studies Conducted using Observational Routinely-collected health Data (RECORD) Statement
